Das Ziel der Regression besteht darin, eine Funktion zu beschreiben, die den Zusammenhang zwischen abhängigen und unabhängigen Variablen eines Datensatzes darstellt.
Prinzip der Regression
Datenvorbereitung
Zu Beginn der Regression müssen die Daten auf gewisse Regeln geprüft werden, wie z.B. die Sinnhaftigkeit aus den gegebenen Daten eine Regression zu erzeugen, sprich ob es überhaupt abhängige Variablen gibt, Denn falls nicht, kann man keine Regression durchführen. Andrerseits muss geklärt werden, wie mit fehlenden Daten umgegangen wird, da diese das Ergebnis beeinflussen können.
Modellerzeugung
Nachdem einer sinnvollen Datenaufbereitung, kann damit begonnen werden ein passendes Modell zu erzeugen. Dabei gibt es bestimmte Verfahren, um die Beziehung zwischen der Abhängigkeit der Variablen darzustellen. Zu diesen zählen unter Anderem:
Lineare Regression
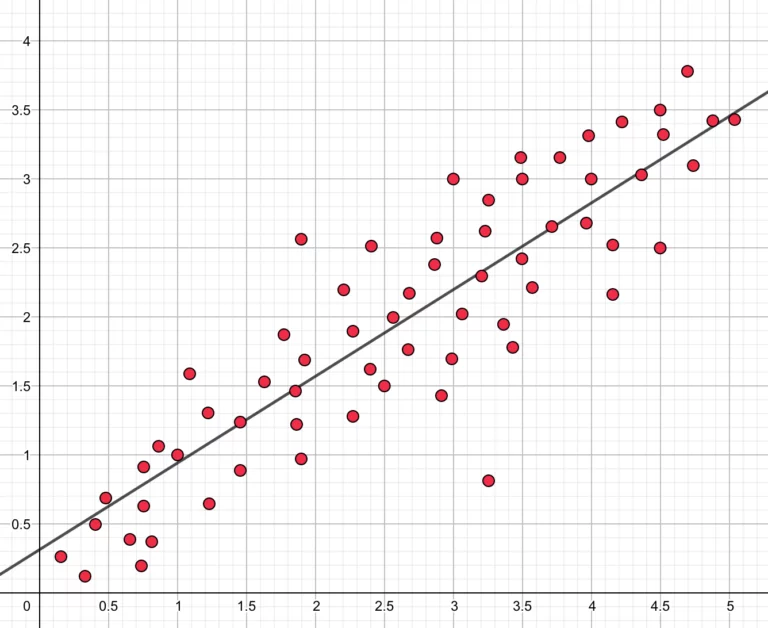
Die lineare Regression ist die einfachste und verständlichste Art der Regression. Hierzu wird eine lineare Abildung mit der allgemeinen Form
y = m * x + b
zwischen dem Input und dem Output erzeugt.
Polynomische Regression
Mit der polynomische Regression ist es möglich nicht lineare Zusammengänge zwischen Verschiedenen Variablen zu beschreiben, wie die Ausbreitung von Krankheitsepidemien. Die allgemeine Form für eine polynomische Rregressionsgleichung ist:
y = a0 * x^0 + a1 * x^1 + a2* x^2 + … + an * x^nLasso
Lasso steht für „Least Absolute Shrinkage and Selection Operator“. Ziel des Verfahrens ist, eine Funktion mit möglichst wenig Koeffizienten zu bilden. Dies geschieht durch einen Parameter, der die Anzahl der Koeffizienten einschränkt. Dabei werden Koeffizienten, die einen geringen Beitrag zur Darstellung der Regression haben, gegen 0 gehen. Dadurch wird die Funktion immer kleiner und somit auch genereller. Durch dieses Verfahren lässt sich bestimmen, welche Variablen einen nur geringen Einfluss auf das Ergebnis haben.
Neuronale Netze
Neuronale Netze können die Zusammenhänge der unabhängigen Variable selbst erlernen. Diese bietet im Vergleich zu statistischen Modellen Vorteile, da man komplexe Zusammenhänge nicht speziell programmieren muss. Weitere Informationen zur Funktionsweise haben wir in unserem Blogbeitrag „Was sind künstliche neuronale Netze?„.
Anwendung
Mit dem Regressionsmodell ist es möglich unbekannte Daten aus einem Datensatz vorherzusagen. Es ergeben sich eine Vielzahl von Anwendungsfällen wie beispielsweise die Vorhersage des Treibstoffverbrauchs eines Fahrzeugs, in Abhängigkeit zu seinem Geweicht und Geschwindigkeit, oder die Produktion von Gütern in Abhängigkeit der eingesetzten Mittel. Außerdem lassen sich durch die Regression Studien auswerten, wie z.B. der Zusammenhang von Tabakkonsum und einer daraus resultierenden erhöhten Sterblichkeitsrate.





