Classification methods divide objects into predefined categories according to their characteristics with the help from classifiers. A classifier is a function that maps an input to a class and its aim is to find suitable rules to which the data can be assigned to the respective class. Normally this is done in machine learning by using a Supervised Learning approach. In the following article, we briefly introduce the most common machine learning methods for solving classification problems.
Decision Trees
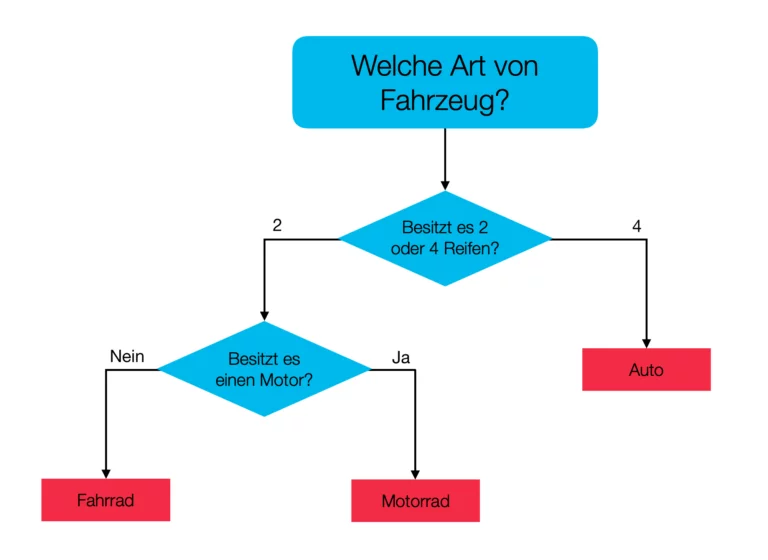
Decision trees in their simplest form can be visualized by thinking of a regular tree; they represent a flow chart like structure where each node represents a “test” on an attribute, each branch represents the outcome of the test, and each leaf node represents a class label. The paths from the root to the leaf represent the predefined rules for your classification methods.
The Bayes Classifier
The Bayes classifier assigns objects to the class to which they most likely belong. The basis for calculating this probability is called a cost function. This represents the objects as vectors, in which each trait is mapped to a dimension, then the cost function determines the probability that a single trait of the object belongs to a class. The individual traits are considered independently of each other. Finally, the object is assigned to the class whose individual traits most closely match a class.
k-Nearest-Neighbors
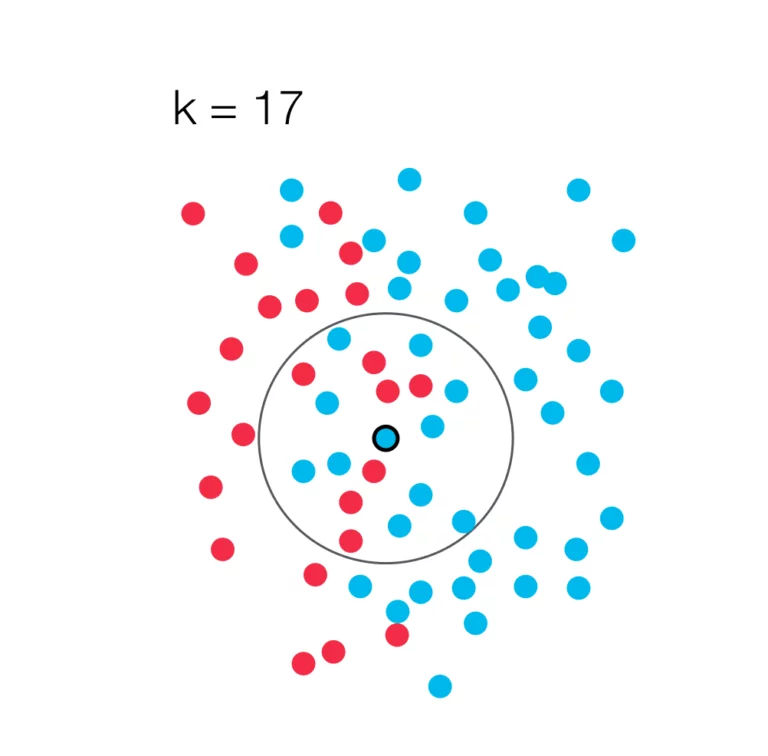
The k-nearest-neighbors method determines the affiliation of an object to a class, taking into account the majority principle meaning that an object is added to the class that is most strongly represented in its neighborhood. To determine the distances between two objects, the Euclidean distance is often used. However, there are alternatives, such as the Manhattan metric, which in certain circumstances may work better. A commonly used method to find a suitable k is to run the algorithm with different values for k and then use the most suitable value. As a general rule, it should be noted that a multi-dimensional space can be used instead of a two-dimensional space.
Support Vector Machine
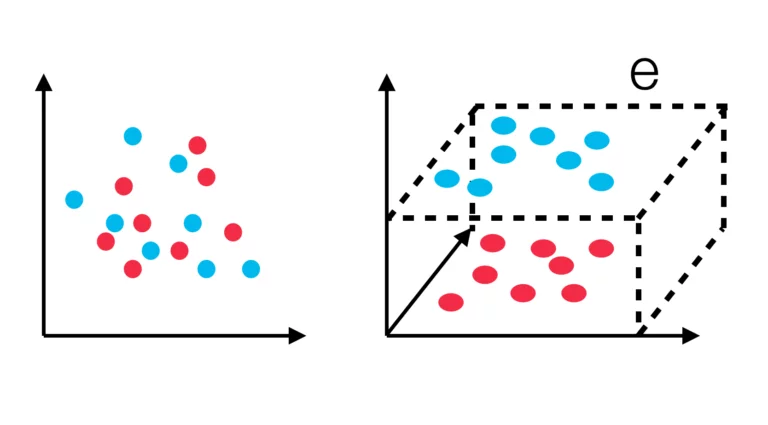
The Support Vector Machine represents each object as a vector in an n-dimensional vector space. Especially for training data that is not linear separable, this is important so that the vectors can be separated by a plane. To separate the different vectors linearly, you choose a hyperplane so that the vectors are as far away from it as possible. Further objects are then classified according to their position in this hyperspace. In the example shown above, the original two-dimensional vectors are mapped into a three-dimensional space. As can be seen, the vectors in two-dimensional space cannot be separated linearly but the three-dimensional space, however, it is possible to place a plane “e” in such a way that the two sets can be separated linearly.
Neural Networks
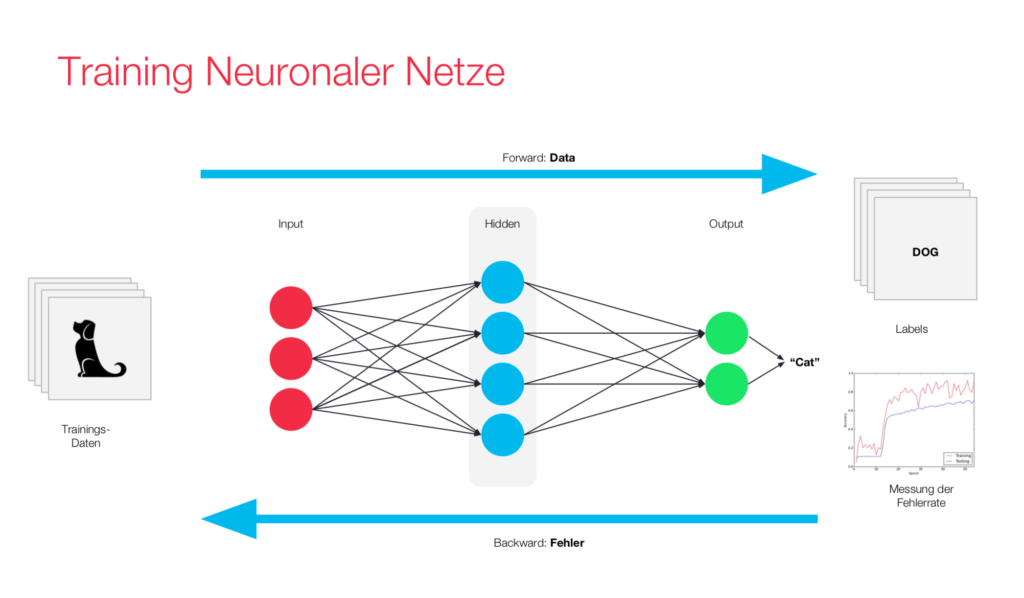
With neural networks, it is possible to classify content in images such as objects, faces, and places with a high degree of certainty if sufficient training data is available. Object recognition has been becoming increasingly popular within the scope of neural networks because of its ability to achieve very good results. Our blog entry on neural networks shows this method in detail.
Challenges of Classification
When choosing the appropriate classifier, the following characteristics must be taken into account:
Accuracy
The accuracy of the classification depends on the rules used. It must be remembered that the accuracy on the training data versus the untrained data is usually different, so it is always possible that a machine learning model produces perfect results for the training data but not for the test data. However, it is possible that poor accuracy is only achieved when classifying new data. In the end, the ratio of correctly classified objects determines the accuracy of the model.
Speed
Under certain circumstances, the speed of classification can be an important criterion for a model. For example, a classifier may achieve 90% accuracy in one-hundredth of the time compared to a classifier that achieves 95% accuracy. So it may be better to do without accuracy if you can achieve an improvement in speed instead.
Comprehensibility
It may be important that it is easy to understand how a classifier arrives at its end result. Even if the result is accurate and fast, above all, people working with the model must have confidence that the model produces a valid result (ie; when making important business decisions)
Application
The use of classification offers many exciting applications in diverse disciplines, such as computer vision; where the aim is to give a computer a visual understanding of the world, which, in turn, is used in various aspects such as self-propelled cars and object recognition. The use of machine learning has many other uses as well, for example, the ability to classify spam/non-spam emails or even in the field of medicine for the early detection of diseases.





