Machine Learning is about the use and development of computer systems that are able to learn and adapt without following explicit instructions. To do this, they use algorithms and statistical models to analyze patterns in data and independently draw conclusions for future analyses. The results of such model training can subsequently be used to make predictions (with unknown data).
A model is a distilled representation of what a machine learning system has learned. Such a model is a mathematical function:
- It takes a query in the form of the input data,
- makes a prediction about it
- and, on the basis of this, provides an answer to a specific question.
Programming and training (with known data sets) of the algorithm is the first important step. Checking whether it can also be applied to unknown data sets – and thus in practice – is the second. Because only through this verification do we subsequently know whether the model actually works and we can trust its predictions. Otherwise, it could be that the algorithm merely learns the data it is fed by heart (overfitting) and is subsequently unable to make reliable predictions for unknown data sets.
In this article, we will point out two of the most common problems of model validation – overfitting and underfitting. And how you can avoid them:
Table of contents:
- What is Model Validation (and for which purposes does it serve)?
- What is Overfitting (and Underfitting)?
- How can Overfitting and Underfitting be Reduced?
- What are the Different Methods of Model Validation?
1. What is Model Validation (and for which purposes does it serve)?
Definition: Model validation describes the process of checking a statistical or data analytic model for its performance.
It is an essential part of the model development process and helps to find the model that best represents your data. It is also used to assess how well this model will perform in the future. Conducting this assessment on the datasets used for training is not appropriate, as it can easily lead to over-optimistic and overfitted models (overfitting).
2. What is Overfitting (and Underfitting)?
Overfitting refers to a model that over-models the training data. In other words, it is too specific to its training data set.
Overfitting occurs when a model learns the details and noise (random fluctuations) in the training data to an extent that negatively affects its performance on new/unknown data. This is indicated by the noise being picked up and learned as a concept. The problem with this is that these concepts do not apply to new data and thus negatively impact the generalization ability (applicability to any unknown data set) of the model.
Low error rates and high variance are strong indicators of overfitting. It is more likely in non-parametric and non-linear models, which have more flexibility in learning a target function. Therefore, many non-parametric machine learning algorithms include parameters or techniques to restrict how much detail the model should learn.
Decision trees, for example, are a non-parametric machine learning algorithm that is very flexible. Therefore, overfitting of the training data often occurs with these. However, this problem can be solved by trimming a tree after learning to remove some of the details it picked up during the learning process.
In addition, overfitting often occurs when the training dataset is relatively small and the model is relatively complex at the same time. A model that is too complex can quickly reproduce the training data too accurately – conversely, a model that is too can never reproduce the training model accurately (this is called underfitting).
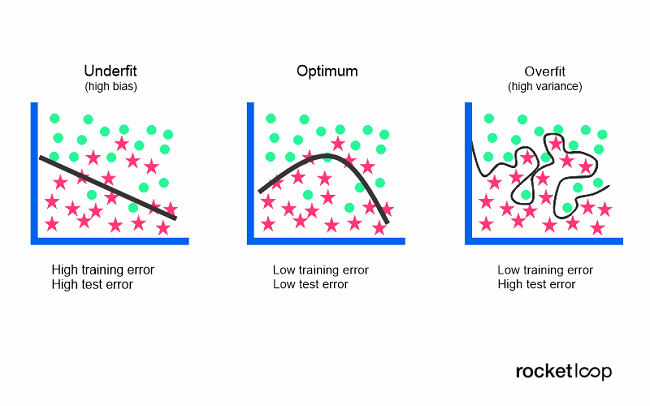
A data model that is too simple is usually not able to accurately capture the relationship between the input and output variables. This results in a high error rate – both with the training data as well as with unknown data sets. A high bias/error rate in combination with a low variance are subsequently strong indicators of underfitting.
Since this behavior can be easily seen during training, underfitted models are usually easier to identify than overfitted ones. The solution to underfitting can be more training time, a more complex model, or less regularization – but more on this in the next section.
Both overfitting and underfitting lead to insufficient generality of a model. However, if a model cannot be reliably applied to unknown data, then it cannot be used for classification or prediction tasks either. The generalized application of a model to new data is ultimately what allows us to use machine learning algorithms to make predictions and classify data.
So the challenge is to keep the model as simple as possible on the one hand, but not too simple on the other. A perfect model – that is, one in which there is neither overfitting nor underfitting – is almost impossible to create. There are, however, various methods and tools with which these negative effects can be excluded with high probability. You will find out which these are in the next chapter.
3. How can Overfitting and Underfitting be Reduced?
There are various methods to avoid overfitting and underfitting as much as possible when training a model. We have listed the most important of these below.
Preventing Overfitting in Machine Learning:
a) Shorter training time (early stopping): With this method, you stop the training before the model learns too many details (including the noise) of the data set. With this approach, however, there is a risk that the training process is stopped too early – which in turn leads to the opposite problem of underfitting. Finding the “sweet spot” between underfitting and overfitting is thus the ultimate challenge.
b) Train with more data: Extending the training set with more data can increase the accuracy of the model by giving it more opportunities to filter out the significant relationship between the input and output variables. However, this is only an effective method if you input only clean and meaningful data. Otherwise, you only add unnecessary complexity to the model, which will ultimately lead to overfitting.
c) Data augmentation: While it is theoretically the best practice to use only clean and informative training data, sometimes noisy data is deliberately added to make a model more stable. However, this method should be used sparingly (as well as, most importantly, only by experienced users).
d) Feature selection: Here you identify the most important features of the training data in order to subsequently eliminate the irrelevant – and thus redundant – ones. This is often confused with dimension reduction, but is a different approach. However, both methods help you to simplify a model to identify the dominant trend within the data.
e) Normalization: This is related to the previous point of feature selection, as it is used to determine which characteristics should be eliminated. To do this, you apply a “penalty” to the input parameters with the larger coefficients, which subsequently limits the variance in the model. There are a number of normalization methods (e.g. L1 and Lasso regularisation or Dropout) – but they all have the same goal: to identify and reduce noise in the data.
f) Ensemble methods: These consist of a set of classifiers (such as decision trees). You combine their predictions to determine the most favorable result. The best-known ensemble methods are Bagging and Boosting.
Preventing Underfitting in Machine Learning:
a) Longer training time: Just as shortening the training phase reduces overfitting, lengthening it reduces underfitting. As mentioned earlier, the challenge is therefore to select the optimal duration of the model training.
b) Feature selection: If there are not enough predictive features, add more of them – or ones with stronger significance. For example, in a neural network, you could add more hidden neurons. And in a forest, more trees. This adds complexity to the model, which leads to better training results – but again only to the point where overfitting starts.
c) Weaken normalization: If you apply the methods for normalizing the training data too strictly, this can lead to the features becoming too uniform. As a result, the model is no longer able to identify the dominant trend, which leads to underfitting. By reducing the regulation, you can introduce more complexity and variation again.
As you can see, finding the balance between underfitting and overfitting is like a tightrope walk. To make sure that neither of these problems is affecting your model, you need to validate it. There are various methods for evaluating models in data science: The best known of these is certainly the k-fold Cross-Validation. We would like to introduce you to this method – and a few others – in the following section.
4. What are the different methods of model validation?
Model assessment methods are used to
- assess the fit between model and data,
- to compare different models (in the context of model selection),
- and to predict how accurate the predictions (associated with a particular model and data set) will likely be.
The purpose of validation, therefore, is to demonstrate that the model is a realistic representation of the system under study: That it reproduces its behavior with sufficient accuracy to meet the objectives of the analysis. While the techniques for model verification are general, you should be much more precise with the procedure itself. Both for the model in question – as well as for the system in which it is to be applied.
Just as the model development will be influenced by the objectives of the study, so will the model validation itself. We will only present a few of the methods used here – but there are many more. Which one you choose in the end should depend on the specific parameters and characteristics of the model you are developing.
The basis of all validation techniques is to split the data set when training the model. This is done to understand what happens when it is confronted with data it has never seen before. Therefore, one of the simplest methods is the Train-Test-Split.
1. Train-Test-Split
The principle is simple: You randomly divide your data into for example about 70% for training and 30% for testing the model. When optimizing according to this method, however, overfitting can easily occur. Why? Because the model searches for the hyperparameters that fit the specific Train-Test you have performed.
To solve this problem, you can create an additional holdout set. This is usually 10-20% of the data that you reserve for later validation and therefore do not use for training or testing. After optimizing your model through the Train-Test-Split, you can then validate with the holdout set whether there is no overfitting.
But what if a subset of our data only contains people of a certain age or income level, for example? Such an (unfavorable) case is called sampling bias. This is a systematic error due to a non-random sample of a data set (such as the population just mentioned) that results in some data points (people) being less likely to be included than others.
2. k-Fold Cross-Validation (k-Fold CV)
To minimize sampling bias, let’s now look at the approach to validation a little bit differently. What if instead of doing one split, we did many splits and validated for all combinations of them?
This is where k-fold Cross-Validation comes into play. It
- splits the data into k foldings,
- then trains the data on k-1 foldings
- and tests on the one folding that was omitted.
This is done for all combinations and the results are then averaged for the individual instances.
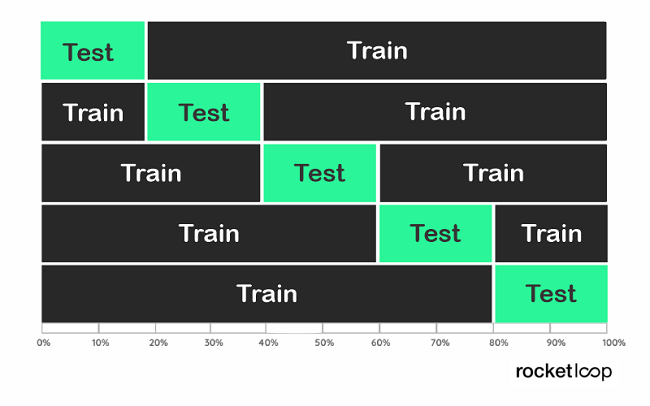
This way all data is used for training as well as for validation. But each data point (each folding) only once. For k, a value between 5 and 10 is typically chosen, as this ensures a good balance between computational effort and accuracy. The advantage of this method is that you get a relatively variation-free performance estimate. The reason for this is that important structures in the training data cannot be excluded.
3. Leave-One-Out Cross-Validation (LOOCV)
This is a special case of cross-validation, where the number of foldings corresponds to the number of instances (observations) in the dataset. The learning algorithm is thus applied once for each instance, using all other instances as the training set and the selected instance as the single-item test set. This procedure is closely related to the statistical method of jackknife estimation.
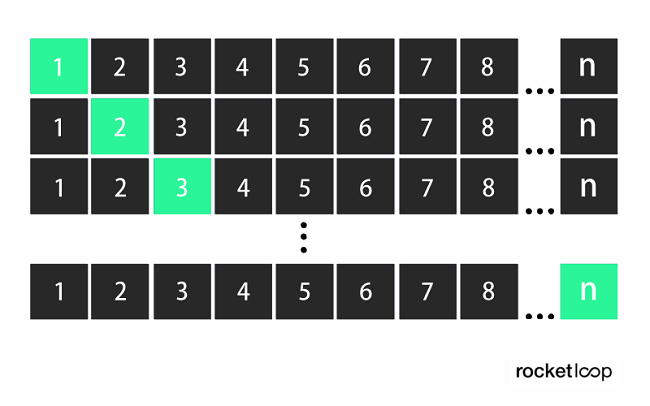
An instance is a case in the training data and is described by a number of attributes. An attribute in turn is an aspect/characteristic of an instance (e.g. age, temperature, humidity).
However, the method is computationally very complex, as the model has to be trained n times. So only use it if the underlying data set is small enough or you have the computing power for a correspondingly large number of calculations.
4. Nested Cross-Validation
Model selection without nested cross-validation uses the same data to adjust the model parameters and to evaluate the model performance, which can lead to an optimistically biased evaluation of the model (overfitting). We get a poor estimate of the errors in the training or testing data due to information leakage.
To overcome this problem, nested cross-validation comes into play, which allows us to separate the step of hyperparameter tuning from the step of error estimation. To illustrate, let’s simply nest two k-fold Cross-Validation loops.
- The inner loop for hyperparameter tuning
- and the outer loop for the estimation of the accuracy.
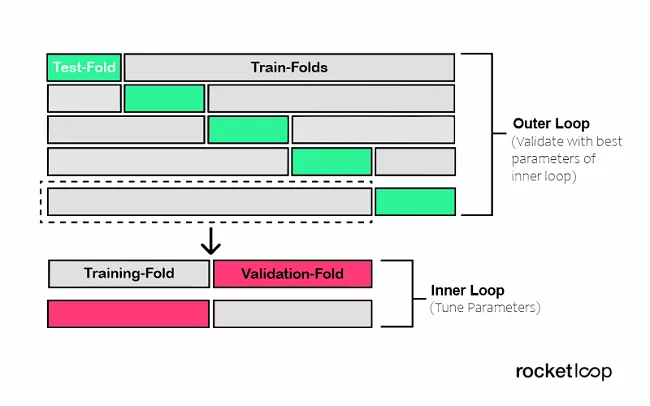
You are free to choose the Cross-Validation approaches for the inner and outer loop. For example, you can use the Leave-One-Out method for both the inner and outer loops, if you want to split by specific groups.
And with that, we have already reached the end of our brief overview of the most important methods for validating a model for Machine Learning. This also brings us to the end of our article on the topic “Problem areas of model validation (and their solutions): overfitting and underfitting!”. We hope that the information and practical examples listed here will be helpful to you for your own software development project.
In case you need any further support, we invite you to contact us and use our experienced team for your software development – we are looking forward to your message. This way you save valuable time for your launch, which you can invest in building your own team. So that you can handle the next product development completely in-house!





