Clustering mit Machine Learning - Ein ausführlicher Leitfaden

Unter dem Begriff Clustering (mit Machine Learning / maschinellen Lernen) versteht man das Zusammenfassen von Daten zu Gruppen: Den namensgebenden Clustern. Diese werden im Gegensatz zur Klassifizierung nicht durch bestimmte gemeinsame Merkmale vorgegeben, sondern ergeben sich auf Grund der räumlichen Ähnlichkeit der betrachteten Objekte (Datenpunkte / Beobachtungen). Mit Ähnlichkeit ist dabei der räumliche Abstand der Objekte, als Vektoren dargestellt, gemeint. Es gibt verschiedene Verfahren diesen Abstand zu bestimmen, wie z.B. die euklidische oder die Minkowski-Metrik.

Dieser Umstand weist allerdings schon darauf hin, dass es keine einheitliche und eindeutig festgelegte Methodik zur Clusterbestimmung gibt. In diesem Beitrag 

1. wollen wir dir deshalb die verschiedenen Methoden und Algorithmen zur Clusteranalyse, sowie deren Vor- und Nachteile, vorstellen.
2. Außerdem schauen wir uns Anwendungen für das Clustering (inklusive deren Problemfeldern)
3. plus ein konkretes Beispiel für eine Clusteranalyse an.

Damit kannst du dir Dein eigenes Bild davon machen, welche von diesen am besten für Deine eigene Clusteranalyse (beim Machine Learning) geeignet ist. Doch nun genug der langen Vorrede und viel Spaß beim Durchlesen - sowie Fortbilden.

Inhaltsverzeichnis:

1. Was ist die Clusteranalyse (Clustering)?
2. Was ist ein Cluster?
3. Welche Methoden (und Algorithmen) gibt es für die Clusteranalyse?
   • Hierarchisches Clustering
   • Partitionierendes Clustering (centroid-based / schwerpunktbasiert)
   • Dichtebasiertes Clustering (density-based)
   • Verteilungsbasiertes Clustering (distribution-based)
4. Validierung von Clusteringergebnissen
5. Anwendungen der Clusteranalyse für das Machine Learning
6. Beispiel für eine Clusteranalyse
7. Hürden des Clusterings beim Machine Learning

1. Was ist die Clusteranalyse (Clustering)?

Die Clusteranalyse (das Clustering) ist eine nicht-überwachte Verfahren des maschinellen Lernens. Sie umfasst die automatische Identifizierung von natürlichen Datengruppen (die Cluster). Ein unüberwachtes Lernverfahren ist eine Methode, bei der wir Rückschlüsse aus Datensätzen ziehen, die aus Eingabedaten ohne gelabelte Antworten bestehen - bei der Verwendung von gelabelten Datensätzen würde es sich hingegen um die bereits angesprochene Klassifizierung handeln. 

Im Gegensatz zum überwachten Lernen (wie der prädiktiven Modellierung), interpretieren Clustering-Algorithmen also lediglich die eingegebenen Daten. Auf Basis von dieser Analyse ermitteln sie dann in weiterer Folge die bereits erwähnten natürlichen Gruppen im gewählten Merkmalsbereich. Dazu werden die verwendeten Datenpunkte (Beobachtungen) einzeln ausgewertet, um jeden von diesen einer bestimmten Gruppe zuzuordnen. 

• Demzufolge sollten Datenpunkte, die sich in der gleichen Gruppe befinden, ähnliche Eigenschaften und / oder Merkmale besitzen. 
• Datenpunkte in verschiedenen Gruppen hingegen sehr unterschiedliche.

Clustering-Techniken kommen wie bereits erwähnt dann zur Anwendung, wenn keine Klassifizierung vorgegeben werden soll, sondern die Daten in natürliche Gruppen eingeteilt. Sie stellen oftmals den ersten Schritt auf dem Weg zum Verständnis von Datensätzen dar.

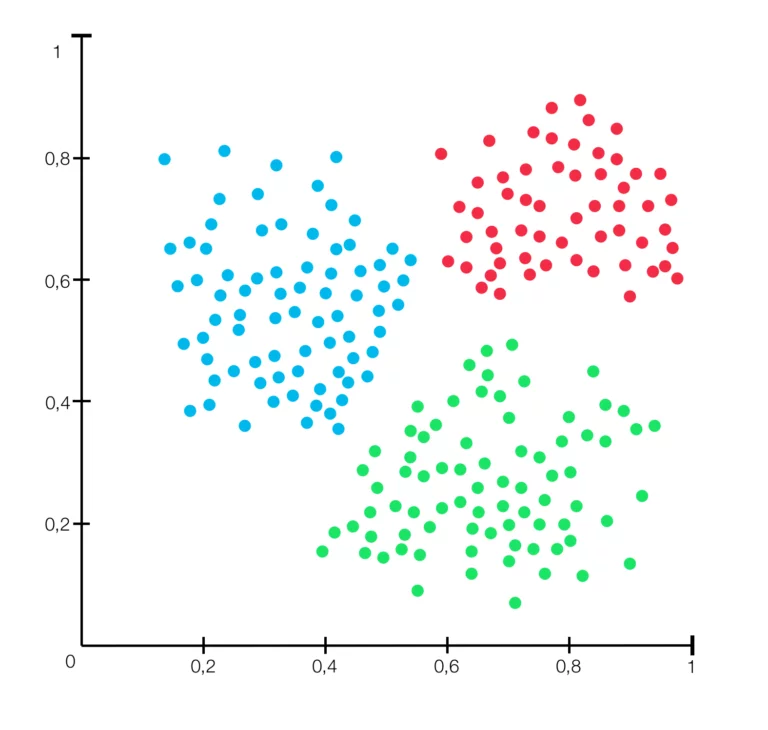
Clustering kann bei der Datenanalyse zu Erkenntnisgewinnung und Mustererkennung benutzt werden, um mehr über die untersuchte Datendomäne zu erfahren.  Clustering kann auch als eine Art von Feature-Engineering nützlich sein, bei dem vorhandene und neue Datenpunkte gemeinsam abgebildet und zu einem bereits identifizierten Cluster zugeordnet werden können. Weitere Anwendungsmöglichkeiten der Clusteranalyse beim maschinellen Lernen sind beispielsweise:

• Marktsegmentierung,
• Analyse sozialer Netzwerke,
• Gruppierung von Suchergebnissen,
• medizinische Bildverarbeitung,
• Bildsegmentierung
• oder auch Anomalieerkennung.

Die Bewertung von identifizierten Clustern ist oftmals subjektiv und kann einen erfahrenen Experten erfordern, obwohl es prinzipiell verschiedenste quantitative Messgrößen und -technikengibt. Typischerweise werden solche Clustering-Algorithmen deshalb zuerst experimentell an theoretischen Datensätzen mit vordefinierten Clustern erprobt, um deren praxistauglichkeit zu ermitteln.

2. Was ist ein Cluster? 

Die Definition für den Begriff "Cluster" kann nicht genau festgelegt werden. Das ist einer der Gründe dafür, warum es so viele Clustering-Algorithmen gibt. Es gibt jedoch einen gemeinsamen Nenner: Eine Gruppe von Datenpunkten mit ähnlichen Eigenschaften und / oder Merkmalen. Des Weiteren sollten die folgenden Voraussetzungen zur Clusterbildungerfüllt sein:

1. Datenpunkte, die sich im selben Cluster befinden, müssen sich so ähnlich wie möglich sein
2. Datenpunkte, die sich in verschiedenen Clustern befinden, müssen so unterschiedlich wie möglich sein.
3. Die Metriken für Ähnlichkeit und Unterschiedlichkeit müssen eindeutig festgelegt sein, sowie einen konkreten Bezug zur Praxis haben.

Allerdings verwenden verschiedene Ansätze (wie bereits angesprochen) verschiedene Clustermodelle - und für jedes von diesen können wiederum verschiedene Algorithmen angegeben werden. Der Begriff eines Clusters, wie er von verschiedenen Algorithmen gefunden wird, variiert dabei erheblich in seinen Eigenschaften. Die wichtigsten Algorithmen / Methoden zur Clusteranalyse (inklusive den daraus resultierenden Clustertypen) haben wir Dir in den folgenden Kapiteln aufgeführt.

3. Welche Methoden (und Algorithmen) gibt es für die Clusteranalyse? 

Für die Clusteranalyse gibt es verschiedenste Ansätze, welche jeweils ihre eigenen Vor- und Nachteile besitzen. Außerdem führen sie zu verschiedenen Ergebnissen - sprich Klassen von Clustern. Als Grundlage für das Clustering verwenden sie jedoch alle Distanz (Unähnlichkeit) und Ähnlichkeit. Bei quantitativen Merkmalen wird dabei die Distanz bevorzugt, um die Beziehung zwischen den einzelnen Datenpunkten zu erkennen. Die Ähnlichkeit wiederum wird bevorzugt, wenn es um qualitative Merkmale geht. 

Außerdem folgt jede Methode zur Clusteranalyse den folgenden grundlegenden Schritten

1. Merkmalsextraktion und -auswahl: Extraktion und Auswahl der repräsentativsten Merkmale aus dem ursprünglichen Datensatz.
2. Entwurf des Clustering-Algorithmus: Entsprechend den Eigenschaften der Problemstellung, welche mit der Datenanalyse behandelt wird.
3. Ergebnisauswertung: Auswertung der erhaltenen Cluster und Beurteilung der Gültigkeit des Algorithmus.
4. Ergebnisinterpretation: Was ist die praktische Erklärung für das Clustering-Ergebnis?

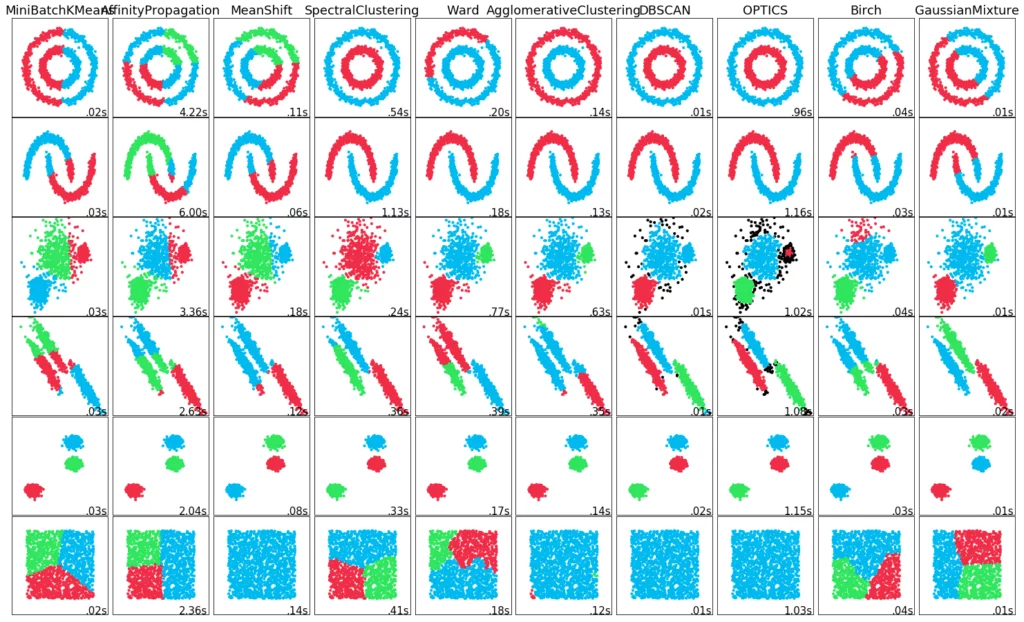
Meistens muss man, um die besten Ergebnisse für einen Datensatz zu erzielen, verschiedene dieser Verfahren mit unterschiedlichen Parametern ausprobieren und sich danach für eines entscheiden. Es existiert nämlich kein Verfahren, dass allgemein am besten funktioniert. Zu den häufig vorkommenden Unsupervised Learning Verfahren zählen:

3a) Hierarchisches Clustering (hierarchical)

Die Grundidee dieser Art von Clustering-Algorithmen besteht darin, die hierarchische Beziehung zwischen den Daten zu rekonstruieren, um sie zu basierend auf dieser zu gruppieren. Dabei wird zu Beginn entweder die Menge aller Datenpunkte gesamt (top-down / ein einzelner großer Cluster) oder die Menge aller einzelnen Datenpunkte (bottom-up / ein einzelner Cluster für jeden Datenpunkt) als Cluster angenommen. 

1. Beim Top-Down-Verfahren wird der zentrale Cluster in weiterer Folge dadurch aufgeteilt, dass der am weitesten von dessen Zentrum entfernte Datenpunkt als zweites Clusterzentrum ausgewählt wird. Danach ordnet der Algorithmus alle anderen Datenpunkte dem jeweils näher liegenden Zentrum zu, wodurch sich zwei getrennte Cluster formen. Dieser Prozess kann dann noch weiter fortgesetzt werden, um die Anzahl der Cluster zu erhöhen.
2. Beim Bottom-Up-Verfahren werden die räumlich am nächsten liegenden Cluster zu einem jeweils neuen zusammengefasst, um so deren Anzahl schrittweise zu reduzieren.

With both methods, it is difficult to define the way in which the distance between the individual data points is determined. On the other hand, how far do you want to divide or combine the clusters. Finally, one should not repeat the process until as many clusters as individual data points or only one cluster remains – and thus end up at the beginning of the respective another approach (top-down / bottom-up).

Das hierarchische Clustering erstellt eine Baumstruktur und ist damit (wenig überraschend) gut geeignet für hierarchische Daten, wie z. B. Taxonomien. Typische Algorithmen sind hierbei beispielsweise BIRCH, CURE, ROCK oder auch Chameleon.

Vorteile und Nachteile von hierarischen Clustering-Methoden für das Machine Learning:

Vorteile:

• Geeignet für Datensätze mit beliebigen Merkmalstypen. 
• Die hierarchische Beziehung zwischen den Clustern lässt sich leicht erkennen.
• Die Skalierbarkeit ist im Allgemeinen relativ hoch.

Nachteile:

• Relativ hohe Zeitkomplexität im Allgemeinen.
• Die Anzahl der Cluster muss voreingestellt werden.

3b) Partitionierendes Clustering (centroid-based / schwerpunktbasiert)

Beim partitionierenden Clustering wird zunächst eine Zahl k festgelegt, die die Anzahl der Cluster vorgibt. Auf Basis von dieser bestimmt der jeweilige Algorithmus k Clusterzentren. Im Anschluss werden die so erhaltenen Zentren derart verschoben, dass die Metrik der Datenpunkte zu ihrem nächstgelegenen Clusterzentrum minimiert wird. Das schwerpunktbasierte Clustering organisiert die Daten somit im Gegensatz zum hierarchischen Clustering in nicht-hierarchischen Clustern.

Die Grundidee dieser Art von Clustering-Algorithmen ist es, das Mittel zwischen den Datenpunkten als Zentrum des jeweiligen Clusters zu betrachten. K-means und K-medoids sind die beiden bekanntesten solcher Algorithmen. Die Kernidee von K-means besteht z.B. darin, das Zentrum des Clusters durch iterative Berechnung fortlaufend zu aktualisieren. Dieser iterative Prozess wird dabei so lange fortgesetzt, bis bestimmte Konvergenzkriterien erfüllt sind. Weiteretypische Clustering-Algorithmen, die auf Partitionierung basieren, sind PAM, CLARA oder CLARANS.

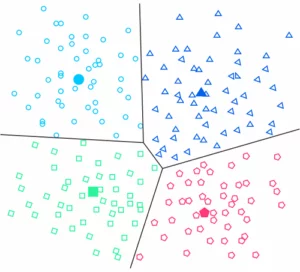
Vorteile und Nachteile von schwerpunktbasierten Clustering-Methoden für das Machine Learning:

Vorteile:

• Relativ geringe Zeitkomplexität und allgemein hohe Recheneffizienz. 
• Die Zugehörigkeit der einzelnen Datenpunkte zu einem Cluster ist während der Clusterbildung veränderbar.

Nachteile:

• Nicht geeignet für nicht-konvexe Daten. 
• Relativ empfindlich gegenüber Ausreißern. 
• Wird leicht in ein lokales Optimum gezogen. 
• Die Anzahl der Cluster muss voreingestellt werden. Deshalb muss man, um optimale Ergebnisse zu erzielen, den Algorithmus mit verschiedenen Werten ausführen und anschließend einen von diesen auswählen.
• Das Clustering-Ergebnis ist abhängig von der Anzahl der Cluster.

3c) Dichtebasiertes Clustering (density-based)

Die Grundidee dieser Art von Clustering-Algorithmen ist, dass Datenpunkte, die sich in einer Region mit hoher Datendichte befinden, als zum selben Cluster gehörig betrachtet werden. Zu den typischen dieser Algorithmen gehören DBSCAN, HDBSCAN, OPTICS und Mean-Shift. Die ersten beiden wollen wir an dieser Stelle noch kurz etwas genauer erklären, da wir sie später in unserem Clustering-Beispiel verwenden werden.

Das populärste, der zuvor genannten Verfahren, ist DBSCAN. Bei diesem wird ein Abstand ε zusammen mit einer Zahl k bestimmt. Datenpunkte, die k Nachbarobjekte mit dem Abstand kleiner Epsilon (ε) besitzen, stellen Kernobjekte dar, die zu einem Clusterzentrum zusammengefasst werden. Datenpunkte, die zwar keine Kernobjekte sind, sich aber in der Nähe eines Zentrums befinden, ordnet man dem Cluster hinzu. Datenpunkte, die keinem Cluster zugehörig sind, gelten als Rauschobjekte.

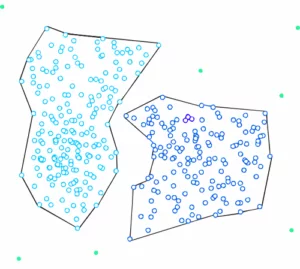
HDBSCAN steht für “Hierarchical Density-Based Spatial Clustering” - und basiert wie bereits erwähnt auf dem DBSCAN-Algorithmus. Er erweitert diesen jedoch, indem er ihn in einen hierarchischen Clusteringalgorithmus überführt. Deswegen benötigt er keinen Abstand ε zur Bestimmung der Cluster. Damit ist es möglich Cluster unterschiedlicher Dichte zu finden und somit eine große Schwachstelle von DBSCAN zu beheben.

Bei der HDBSCAN-Methode wird zunächst eine Zahl k festgelegt. Mit dieser wird bestimmt, wie viele Nachbarschaftsobjekte bei der Bestimmung der Dichte eines Punkts betrachtet werden. Hierin besteht bereits ein entscheidender Unterschied im Vergleich zu DBSCAN. DBSCAN sucht in der gegebenen Distanz ε nach Nachbarn, wohingegen HDBSCAN nach der Distanz sucht, ab welcher k Objekte in der Nachbarschaft liegen.

Nach dieser Zahl k wird die Kerndistanz für jeden Punkt bestimmt. Diese ist die kleinste Distanz, mit der k Objekte erreicht werden können. Außerdem wird eine Erreichbarkeitsmetrik eingeführt. Diese ist definiert als der größte Wert von entweder der Kerndistanz des Punktes A, der Kerndistanz des Punktes B, oder der Distanz von Punkt A zu Punkt B. Mit dieser Erreichbarkeitsmetrik wird anschließend ein minimaler Spannbaum gebildet. 

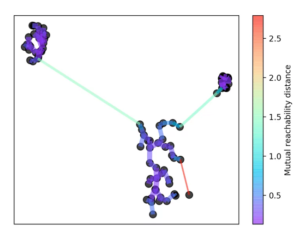
Dazu wird immer die längste Kante aus dem Baum entfernt. Anschließend wird die Hierarchie erstellt, indem in Abhängigkeit zur Distanz die einzelnen Punkte aus dieser herausfallen.

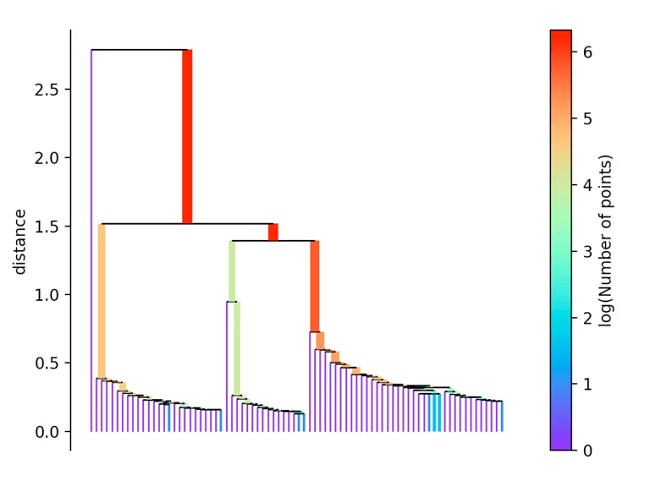
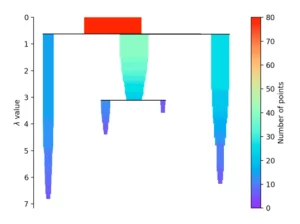
Falls mehr als zu Beginn definierte “min_cluster_size” Punkte bei einer Distanz herausfallen, bilden diese einen neuen Teilbaum. Anschließend wählt das Verfahren die Cluster aus, die die größte Stabilität aufweisen. Diese berechnet sich, in dem man die Summe der Kehrwerte der Distanz, ab welcher ein Punkt aus einem Cluster fällt, für alle Punkte eines Clusters berechnet. Das heißt liegen viele Punkte nahe am Zentrum, hat der Cluster eine hohe Stabilität. Auf dem Bild erkennbar an einer großen Fläche.

Vorteile und Nachteile von dichtebasierten Clustering-Methoden für das Machine Learning:

Vorteile:

• Clustering mit hoher Effizienz. 
• Geeignet für beliebige Datenformate.

Nachteile:

• Führt zu einem Clustering-Ergebnis mit geringer Qualität, falls die Dichte des Datenraums nicht gleichmäßig ist.
• Benötigt einen sehr großen Speicherplatz, falls das Datenvolumen groß ist.
• Das Clustering-Ergebnis ist sehr empfindlich gegenüber den voreingestellten Parametern.

3d) Verteilungsbasiertes Clustering (distribution-based)

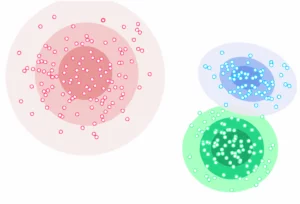
Dieser Clustering-Ansatz geht davon aus, dass die Daten aus Verteilungen (wie z. B. der Gauß-Verteilung) bestehen. Mit zunehmender Entfernung vom Zentrum einer Verteilung nimmt die Wahrscheinlichkeit ab, dass ein Datenpunkt zu dieser gehört. Voraussetzung für eine verteilungsbasierte Clusteranalyse ist immer, dass mehrere Verteilungen im Datensatz vorliegen. Typische Algorithmen sind hier DBCLASD und GMM.

Die Kernidee von GMM ist, dass der Datensatz aus mehreren Gauß-Verteilungen besteht, die aus den Originaldaten generiert werden. Und die Daten, die derselben unabhängigen Gauß-Verteilung gehorchen, als zum selben Cluster gehörend betrachtet werden.

Vorteile und Nachteile von verteilungsbasierten Clustering-Methoden für das Machine Learning:

Vorteile:

• Realistischere Werte für die Wahrscheinlichkeit der Zugehörigkeit.
• Relativ hohe Skalierbarkeit durch die Änderung der angewandten Verteilung und damit Anzahl der Cluster.
• Statistisch gut belegbar.

Nachteile:

• Grundannahme ist nicht hundertprozentig korrekt. 
• Sehr viele Parameter, die einen starken Einfluss auf das Clustering-Ergebnis haben. 
• Relativ hohe zeitliche Komplexität.

Das war der Überblick über die wichtigsten Clusteringverfahren beim maschinellen Lernen. Es kann allerdings schwer sein ein Clusteringergebnis objektiv zu bewerten, da der Algorithmus ja prinzipiell automatisiert Cluster finden soll. Denn gäbe es bereits eine Einteilung der Datenpunkte in Gruppen, wäre das Clustering überflüssig. Da diese Gruppeneinteilung aber nicht bekannt ist, muss das vom Algorithmus ermittelte Resultat im Anschluss kritisch bewertet werden. Dazu stehen verschiedene Methoden Zur Verfügung, mit denen sich bessere von schlechteren Ergebnissen unterscheiden lassen. Im folgenden Kapitel wollen wir Dir die gängigsten von diesen etwas genauer vorstellen.

4. Validierung von Clusteringergebnissen

Zur Bewertung der Ergebnisse einer Clusteranalyse - vor allem hinsichtlich der Anzahl der erhaltenen Cluster - gibt es wie bereits erwähnt verschiedene Methoden. Einige der gebräuchlichsten von diesen findest du im Folgenden im Detail erklärt.

4a) Elbow criterion

Das Elbow-Kriterium eignet sich sehr gut dazu, um bei einem K-means-Clustering die optimale Anzahl von Clustern zu bestimmen. Dabei trägt man in einem Diagramm auf der x-Achse die Anzahl der Cluster, sowie auf der y-Achse die Summe der quadrierten Abweichungen der einzelnen Punkte zum jeweiligen Clusterzentrum auf. Falls auf dem so entstandenen Diagramm ein Knick (der Ellbogen) erkennbar sein sollte, ist dieser Punkt die optimale Anzahl an Clustern. Ab diesem sinkt nämlich die Aussagekraft der einzelnen Cluster, da sich die Summe der quadrierten Abweichungen nur noch leicht verändert.

Die Verwendung des "Ellbogens" oder "Knies einer Kurve" als Grenzpunkt ist eine gängige Vorgehensweise in der mathematischen Optimierung, um einen Punkt zu wählen, an dem abnehmende Erträge die zusätzlichen Kosten nicht mehr wert sind. Beim Clustering bedeutet dies, dass man eine Anzahl von Clustern wählen sollte, bei der das Hinzufügen von weiteren Clustern keine wesentlich bessere Modellierung der Daten mehr ergibt.

Theoretisch verbessert das Erhöhen der Anzahl von Clustern natürlich die Anpassung, da mehr der Variation erklärt wird. Das mehr an Parametern (mehr Cluster) ist jedoch ab einem bestimmten Punkt eine Überanpassung, was der Knick im Diagramm widerspiegelt. Bei Daten, die tatsächlich aus k definierten Gruppen bestehen - z.B. k Punkte, die mit Rauschen abgetastet wurden - wird das Clustering mit mehr als k Clustern mehr der Variation "erklären" (da es kleinere, engere Cluster verwenden kann). Die Überanpassung besteht allerdings darin, dass die definierten Gruppen in weitere Sub-Cluster unterteilt werden. 

Das beruht darauf, dass die ersten Cluster viel Information hinzufügen (viel Variation erklären), da die Daten tatsächlich aus so vielen Gruppen bestehen - demzufolge sind diese Cluster notwendig. Sobald die Anzahl der Cluster jedoch die tatsächliche Anzahl der Gruppen in dem verwendeten Datensatz übersteigt, nimmt der Informationsgehalt stark ab.

Das Resultat: Ein scharfer Knick im Graphen, da dieser bis zum Punkt k schnell ansteigt (Unteranpassungsbereich) und danach nur mehr langsam (Überanpassungsbereich). Der Optimalbereich (optimale Anzahl an Clustern) ist also wie bereits eingangs erklärt der Punkt k.

4b) Gap Statistic

Die Gap-Statistik ist ebenfalls eine Methode zur Annäherung an die optimale Anzahl von Clustern (k) für ein unüberwachtes Clustering. Diese beruht darauf, dass wir eine Fehlermetrik (die Summe der Quadrate innerhalb von Clustern) in Bezug auf unsere Wahl von k bewerten. Wir sehen dabei tendenziell, dass der Fehler stetig abnimmt, wenn wir k erhöhen.

Wir erreichen jedoch einen Punkt, an dem der Fehler nicht mehr abnimmt (der Ellbogen im Diagramm). Das ist der Punkt, an dem wir unseren Wert von k als die "richtige" Anzahl an Clustern festlegen wollen. Wir könnten uns zwar rein das Diagramm ansehen und den Ellbogen schätzen - besser geeignet, um dies zu tun, ist jedoch ein formalisiertes Verfahren: Die Gap-Methode.

Wir haben nun dieses Diagramm, das die Fehlerrate (z. B. K-Means WCSS) mit dem Wert von k vergleicht. Wir können nur ein Gefühl dafür bekommen, wie gut jedes Fehler- bzw. k-Wert-Paar ist, wenn wir in der Lage sind, den erwarteten Fehler für k unter einer Null-Referenzverteilung zu vergleichen. Mit anderen Worten: Falls es absolut kein Signal in Daten mit ähnlicher Gesamtverteilung gäbe und wir sie mit k Clustern gruppieren würden, was wäre dann der zu erwartende Fehler?

Mit der Gap-Statistik wollen wir nun den Wert von k finden, für den die Lücke (Gap) zwischen dem erwarteten Fehler unter einer Nullverteilung und unserem Clustering am größten ist. Wenn die Daten echte, sinnvolle Cluster haben, würden wir erwarten, dass diese Fehlerrate schneller abnimmt als die errechnete Rate.

4c) Calinski-Harabasz-Index

Der Calinski-Harabasz-Index (auch bekannt als Varianzverhältniskriterium) ist relativ schnell zu berechnen - und ist das Verhältnis der Varianz der Quadratsummen der Abstände einzelner Objekte zu ihrem Clusterzentrum durch die Quadratsumme der Distanz zwischen den Clusterzentren und dem Mittelpunkt der Daten eines Clusters geteilt. Ein gutes Clusteringergebnis hat dabei einen hohen Calinski-Harabasz-Wert Die Punktzahl ist nämlich höher, falls die Cluster dicht und gut getrennt sind, wie es dem Standardkonzept eines Clusters entspricht.

4d) Silhouette Coefficient (Silhouettenmethode)

Die Silhouettenmethode vergleicht den durchschnittlichen Silhouettenkoeffizienten unterschiedlicher Clusteranzahlen. Der Silhouettenkoeffizient gibt dabei an, wie gut die Orientierung eines Datenpunktes zu seinen beiden nächstgelegenen Clustern A und B ausfällt. Dabei ist der Cluster A derjenige, zu welchem das Objekt zugeordnet wurde.

Der Silhouettenkoeffizient berechnet sich, in dem die Differenz des Abstands des Datenpunktes zum Cluster B zu dem Abstand des Datenpunktes zum Cluster A gebildet wird. Diese Differenz wird anschließend mit der maximalen Distanz des Objekts zu Cluster A und B gewichtet. Dabei kann das Ergebnis S zwischen -1 und 1 liegen. 

1. Falls S < 0 liegt das Objekt näher an Cluster B als an A. Demnach kann das Clustering verbessert werden.
2. Falls S ≈ 0 dann liegt das Objekt in der Mitte von beiden. Somit ist das Clustering wenig aussagekräftig. 
3. Je weiter sich S an 1 annähert, desto besser ist das Clustering. Demzufolge wird bei der Silhouettenmethode nach der Anzahl an Clustern gesucht, für welche der durchschnittliche Silhouettenkoeffizient am höchsten liegt.

5. Anwendungen der Clusteranalyse für das Machine Learning

Da Clustering-Verfahren in der Lage sind abstrakte Zusammenhänge in Daten sichtbar zu machen, welche das menschliche Gehirn nicht so offensichtlich wahrnimmt, finden sie heute in vielen Bereichen des maschinellen Lernens Anwendung. Zu den Anwendungsbereichen gehören beispielsweise: 

1. Marktanalyse: In dieser wird das Clustering verbreitet eingesetzt, um z.B. Daten aus Umfragen auszuwerten. Hierbei werden Kunden in Gruppen eingeteilt, auf welche in weiterer Folge optimale Produkt- oder Werbeplatzierungen zugeschnitten werden.
2. Natural Language Processing (NLP): Hierbei ermöglichen die Clustering-Algorithmen die automatisierte Auswertung von Texten und Sprache. 
3. Kriminalitätsanalyse: Hierbei erlaubt das Clustering eine effizienten Einsatz von Polizei- und Sicherheitskräften, da Kriminalitäts-Hot-Spots besser erkannt und ausgewertet werden können.
4. Bei der Identifizierung von Krebszellen: Die Clustering-Algorithmen teilen dabei die krebsartigen und nicht krebsartigen Datensätze in verschiedene Gruppen ein.
5. Suchmaschinen: Suchmaschinen arbeiten ebenfalls mit der Clustering-Technik. Das Suchergebnis wird dabei basierend auf dem Objekt, das der Suchanfrage am nächsten liegt, kreiert. Dies geschieht, indem ähnliche Objekte in einer Gruppe gruppiert werden, die weit von unähnlichen Objekten entfernt ist. Die Genauigkeit des Ergebnis einer Suchanfrage hängt damit stark von der Qualität des verwendeten Clustering-Algorithmus ab.
6. Biowissenschaften: In der Biologie wird die Clusteranalyse z.B. verwendet, um verschiedene Pflanzen- und Tierarten mit Hilfe der Bilderkennungstechnik zu klassifizieren.
7. Landschaftsplanung: Die Clustering-Technik wird zur Identifizierung von Flächen mit ähnlicher Landnutzung in der GIS-Datenbank verwendet. Dies kann sehr nützlich sein, um z.B. festzulegen, für welchen Zweck eine bestimmte Landfläche genutzt werden sollte - d.h. für welchen sie am besten geeignet ist.

Nachdem wir nun die wichtigsten Anwendungsbereiche der Clusteranalyse im Machine Learning kennengelernt haben, wollen wir uns ein praktisches Beispiel für eine solche im Detail ansehen.

6. Beispiel für eine Clusteranalyse

Um eine beispielhafte Clusteranalyse durchzuführen, müssen wir zuerst einen Datensatz generieren, um dessen Daten anschließend in Cluster einordnen zu können.

6a) Datensatzgenerierung

Unseren Datensatz generieren wir so, dass er aus insgesamt 80 zweidimensionalen Datenpunkten besteht, die in einem festgelegten Radius zufällig um drei zentrale Punkte erzeugt werden. Dafür verwenden wir die Methode “make_blobs” aus scikit-learn.

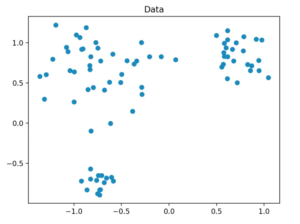
6b) Die verwendeten Clusteringverfahren

Nachdem wir unsere Daten generiert haben, können wir mit dem eigentlichen Clustering beginnen. Dafür verwenden wir die Verfahren k-means, DBSCAN und HDBSCAN. Dabei zählt k-means zu den partitionierenden Verfahren, die übrigen hingegen zu den dichtebasierten. HDBSCAN baut auf DBSCAN auf. Im Detail haben wir die einzelnen in diesem Beispiel verwendeten Algorithmen bereits im Kapitel 3 vorgestellt.

Mit Ausnahme von HDBSCAN entstammen die Verfahren der scikit-learn Bibliothek. Für das HDBSCAN-Verfahren gibt es aber ebenfalls eine vorgefertigte Bibliothek, auf die wir zurückgreifen können. Mit der Methode “fit_predict” von scikit-learn bestimmen wir in weiterer Folge mit jedem Modell die Zugehörigkeit der einzelnen Datenpunkte zu einem Cluster.

6c) Auswertung unseres Clusteranalyse-Beispiels

Für diese verwenden wir den Calinski-Harabasz-Index und die Silhouettenmethode - sowie für das k-means-Clustering speziell das Elbow-Kriterium.

k-means-Clustering:

Wenn wir uns die einzelnen Metriken für dieses anschauen, stellen wir fest, dass die optimale Anzahl an Clusterzentren 3 beträgt. Zwar deutet die Silhouettenmethode darauf hin, dass ein vierter Cluster durchaus sinnvoll wäre - allerdings spricht das Elbow-Kriterium dagegen. Bei diesem bildet ein vierter Cluster nämlich keinen Knick und bietet somit nur einen sehr bedingten Mehrwert. 

Nehmen wir nun noch den Calinski-Harabasz-Index dazu, erkennen wir mit diesem ebenfalls, dass der vierte Cluster nur einen schwach höheren Score erzielt. Daraus folgern wir, dass drei die optimale Anzahl an Clustern für ein k-means Clustering auf unserem Datensatz ist. Dieses Ergebnis ergibt auch durchwegs Sinn, wenn wir bedenken, dass wir unsere Daten um 3 zentrale Punkte herum generiert haben.

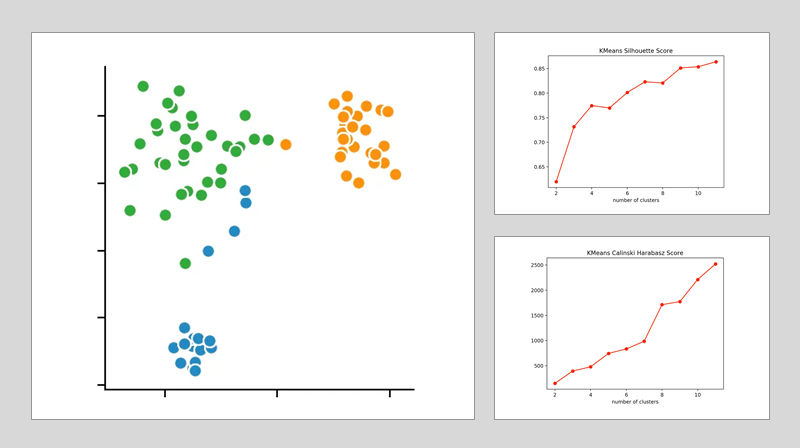
DBSCAN:

Für die beiden anderen Clusteringverfahren können wir die Anzahl der zu findenden Cluster nicht vorher festlegen, sondern lediglich die Parameter bestimmen, nach denen die Algorithmen deren Anzahl auswählen. Für das DBSCAN-Verfahren<legen wir für diesen zweck die Distanz ε<fest und variieren lediglich die Anzahl der minPoints. 

Dabei deutet die Silhouettenmethode auf die Anzahl von vier minPoints hin. Dagegen spricht der Calinski-Harabasz-Index dafür nur drei von diesen festzulegen. Da der Unterschied von drei auf vier in der Silhouettenmethode geringer ausfällt als beim Calinski-Harabasz-Index, entscheiden wir uns dafür, den Wert auf drei festzulegen. Dabei entsteht folgendes Clustering:

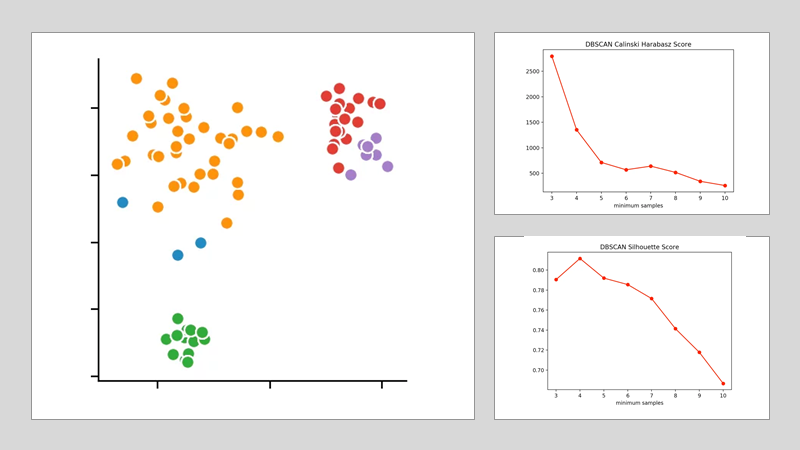
Wir sehen, dass der Algorithmus sich für 4 Clusterzentren entschieden hat. Dabei wird deutlich, dass die DBSCAN-Methode Schwierigkeiten bei unterschiedlich dichten Clustern bekommt.

HDBSCAN:

Beim HDBSCAN-Verfahren variieren wir die kleinste Clustergröße. Das ist die Anzahl an Punkten, die bei einem hierarchischen Verfahren nötig ist, damit ein (oder mehrere) isolierte Datenpunkte als neuer Cluster angesehen werden. Durch die Anwendung des Calinski-Harabasz-Index und der Silhouettenmethode erkennen wir, dass die optimale Größe zwischen vier und fünf Punkten liegt. Wir entscheiden uns für vier und erhalten folgendes Clusteringergebnis.

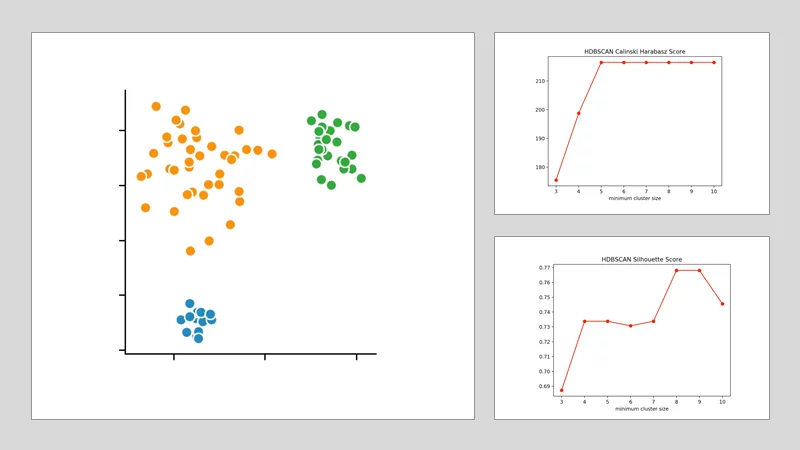
Mit diesem Beispiel sollte deutlich geworden sein, dass es schwierig sein kann, Clusteringergebnisse von einem Datensatz auf ihre Richtigkeit hin zu überprüfen. Es gibt viele weitere Verfahren, die ebenfalls unterschiedliche Lösungen hervorgebracht hätten. Die Metriken zur Validierung der Clusteringergebnisse eignen sich im Einzelnen nur bedingt. Und so ist es stets sinnvoll mehrere von diesen zu Rate zu ziehen und miteinander zu vergleichen. Nur so findest du den geeignetsten Algorithmus für den jeweiligen Anwendungsfall - und kannst alle weiteren Parameter optimal auf diesen abstimmen. 

7. Hürden des Clusterings beim Machine Learning

Das Data Mining versucht Muster in großen Datensätzen zu entdecken. Das Ziel einer Clusteranalyse ist es also, die natürlichen Gruppen innerhalb einer großen Menge von erhobenen Daten (Datenpunkten) festzulegen. Die Anwendung von Clusteringmethoden für das maschinelle Lernen hat dabei zwei große Schwachpunkte: 

1. Bei sehr großen Datensätzen, wird das Schlüsselkonzept des Clustering - der Abstand zwischen den einzelnen Messungen / Beobachtungen - durch den sogenannten Fluch der Dimensionalität unbrauchbar gemacht. Dadurch ist es bei großen Datenmengen sehr zeitaufwändig - besonders, wenn der Raum mehrere Dimensionen besitzt.
2. Unzulänglichkeiten der bestehenden (und verwendeten) Algorithmen. Diese umfassen
   1. die Unfähigkeit zu erkennen, ob der Datensatz homogen ist oder Cluster enthält.
   2. die Unfähigkeit, die Variablen nach ihrem Beitrag zur Heterogenität des Datensatzes zu ordnen.
   3. die Unfähigkeit, spezielle Muster zu erkennen: Clusterzentren, Kernregionen, Grenzen von Clustern, Zonen der Vermischung, Rauschen oder auch Ausreißer.
   4. die Unfähigkeit, die richtige Anzahl von Clustern zu schätzen.
   5. Außerdem ist jeder Algorithmus darauf ausgerichtet, die gleiche Art von Clustern zu finden. Dadurch versagt er, sobald eine Mischung von Clustern mit unterschiedlichen Eigenschaften vorliegt.

Weiters ist die Effektivität des Clusterings durch das gewählte Verfahren der Abstandsmessung bestimmt. In der Regel gibt es kein allgemein richtiges Ergebnis. Das liegt daran, dass dieses in Abhängigkeit der verschiedenen Verfahren mit jeweils verschiedenen Parametern zum Teil drastisch unterschiedlich ausfällt. Dadurch ist es wie in Kapitel 4 ausführlich erläutert teilweise nicht leicht, das Ergebnis zu interpretieren sowie dessen Richtigkeit zu überprüfen. 

Möglichkeiten diese Überprüfung durchzuführen wären, das Resultat des Clusterings mit bekannten Klassifizierungen zu vergleichen oder die Auswertung durch einen menschlichen Experten. Beide Varianten sind aber nur bedingt geeignet, da einerseits das Clustering nicht nötig wäre, wenn es bereits bekannte Klassifizierungen gäbe. Und andererseits menschliche Beurteilungen stets sehr subjektiv ist.

Trotz ihrer Schwächen ermöglichen Clusteringverfahren es jedoch, auch höherdimensionale Daten in homogene Gruppen einzuteilen. Dadurch eignen sie sich sehr gut für die Datenauswertung und -verarbeitung beim maschinellen Lernen. Wichtig ist es nur, immer die gerade genannten Punkte zu berücksichtigen und die erhaltenen Ergebnisse (Cluster) kritisch zu hinterfragen.

Damit sind wir auch schon am Ende unseres Beitrags zum Thema “Clustering beim Machine Learning” angelangt. Wir hoffen, die hier aufgeführten Informationen und Praxisbeispiele sind Dir bei Deinem eigenen Softwareentwicklungsprojekt hilfreich.

Falls du dabei doch etwas Unterstützung benötigen solltest, laden wir Dich ein mit uns Kontakt aufzunehmen, um für Deine Softwareentwicklung auf unser erfahrenes Team zurückzugreifen - wir freuen uns auf Deine Nachricht. So sparst du wertvolle Zeit für Deinen Launch, welche du in den Aufbau Deines eigenen Teams investieren kannst, damit du die nächste Produktentwicklung komplett Inhouse stemmst!